Business Calculus       Use of differential

1. Stock price change
　If the change in stock price can be expressed as a three-dimensional equation, the maximum stock price can be found  by  differentiating it.


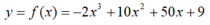
Suppose that the movement of a company's stock price (y) is determined by the following condition (x).
     
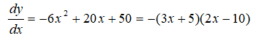
The maximum stock price is at x=-5/3 or x=5. x=-5/3 is not suitable for this example,
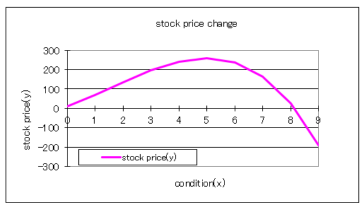
so x=5 and the local maximum=259. f(5)=-2x5^3+10x5^2+50x5+9=259
        　
         
2. Management of rental apartments
　If profit can be expressed as a formula, the maximum profit can be obtained by differentiating it.

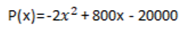
The monthly profit P(x) of a large rental apartment (250 rooms) is calculated by the following formula, where x is the  number of  rooms.

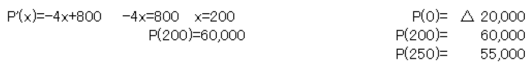
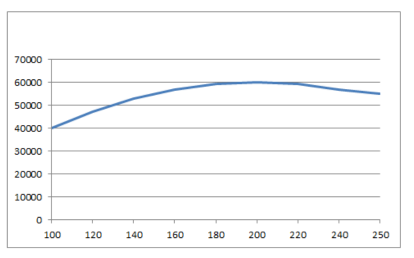
How many rooms should I rent to maximize my monthly profit?
You can see it in the graph below.
                                         
　　　　　　                    
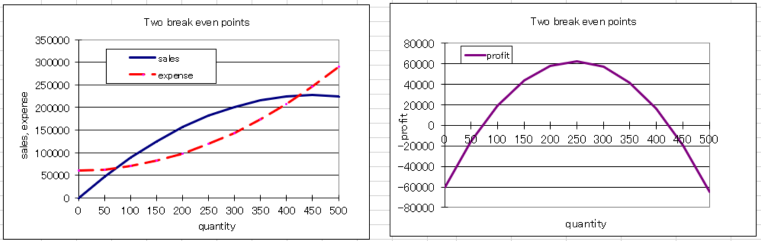
3. Two break-even points
　In the business model of the contract project type such as order receiving software and construction/civil engineering,  it  is often the case that a company will be in the red if it receives an order that is larger than its physical strength. Of  course, even if the project is too small, the fixed cost cannot be recovered and it will be in the red. In other words, there  are two break-even points. In  these industries, "bigger is NOT better!" This can be analyzed well in calculus.
　・Horizontal axis: Business Volume (number of sales, man-hours for services, etc.), not sales
　・Unit sales price: As Volume increases, it gradually decreases (Volume Discount, supply and demand)

[Example]Sales per unit = 1000 -1.1x (Price drops by 0.11% when one unit is sold)
　・Sales:　　
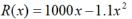
　・Cost: Considers secondary variable cost in addition to primary variable cost (Putnam model, etc.)
　 Cost:
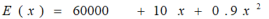
　　　　　60000:Fixed cost     10x:Primary function variable cost   0.9x^2:Secondary function variable cost
　 profit:

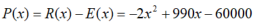
When this quadratic equation is solved, x = 71 or 424, that is, BEP1 = 71, BEP2 = 424 .
The number x that maximizes profit is obtained by differentiating profit P(x).
P'(x)=- 4x+990 x=247.5 When volume x = 248, the maximum profit is 62513.

         
4. Maximize sales
　The price (P, yen) and the number of tickets sold (Q) for a given concert can be predicted as follows.
(If you raise the price, you will sell less. The maximum number of seats in a concert hall is10,000.) What price and number  will maximize sales?　
          
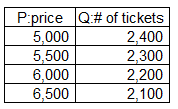
Formulate the relationship between the price (P) and the number of units sold (Q).
Here we use simple regression analysis.
　Calculate sales R = P*Q　
Differentiate sales to obtain sales R' and calculate when the price reaches its maximum.　　　　　　　
  　   
     
        
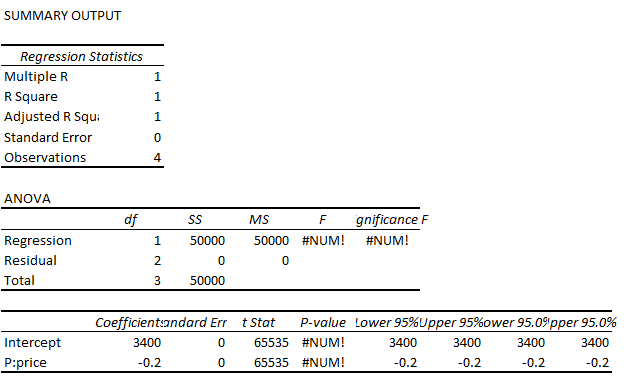
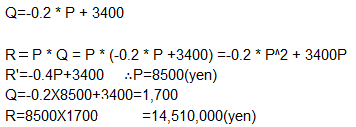
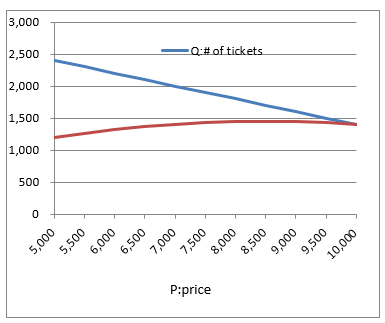
When the price (P) is 8,500yen, the number of tickets sold (Q) will be 1,700, and the maximum sales will be 14,510,000 yen.  

           A quick note on business calculus :  Relationship between differentiation and integration