Business Calculus
Business Calculus
1. The history of calculus
Two important figures appear in calculus, which was established in Europe in the 17th century. Newton, the great British scientist, and Leibniz, the German philosopher and mathematician.
Newton (British:1643-1727: Died 84 years old) Leibniz(Germany: 1646-1716: Died 70 years old)
1704:Newton's"Theory of Quadrature" 1684: Leibniz's "Thesis on Calculus"
They didn't create calculus together. On the contrary, there was a fierce dispute between the academic societies in England and Germany over which of them founded calculus first. Chronologically speaking, Newton was the first to come up with the concept of calculus, but Leibniz was the first to publish it as his paper. British academics therefore accused Leibniz of plagiarizing Newton's unpublished papers. Naturally, Leibniz did not remain silent, and the exchange of violent criticism continued for many years. It is believed that he founded calculus.
Two geniuses of mathematics who lived in the 17th century, Newton died at the age of 84 and Leibniz at the age of 70. In the music world of this era, it was a little before Bach (1685-1750) of "Aria on the G string" was active. In Japan, it is the Genroku era of Tokugawa Tsunayoshi, the fifth Tokugawa shogun. That's right, calculus is "classical mathematics" that was created over 300 years ago.
2. Differentiation
Before we can understand differentiation, we need to understand limits. The limit is "to get as close to XYZ as possible". In the linear function y=x+1, if x approaches 1 as much as possible, y approaches 2 as much as possible. This is called convergence to 2, and 2 is called the limit of y=x+1.
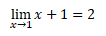
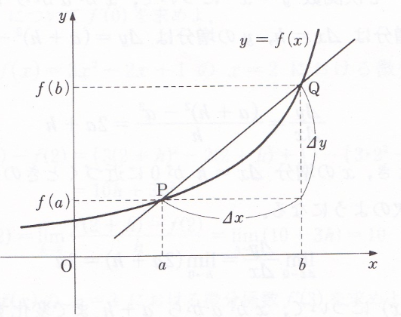
The function y=f(x) is expressed as y=f(a) when x=a. As variable x varies from a to b, y varies from f(a) to f(b).
△y＝f(a+△x)-f(a)
The average rate of change is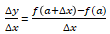
.If the average rate of change converges to a constant value when △x is brought as close to 0 as possible, then this limit value is called the differential coefficient of the function y=f(x) at x=a, f' (a).
f'(a)=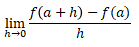
The derivative is the rate of change at point a. For y=f(x), the function f'(x) is called its derived function, and at f'(x) represent. Finding the derivative is called differentiation.
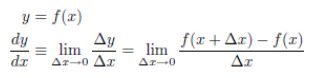
As△x approaches zero, the line approaches the tangent of f(x) at x. To "find a derivative (differentiation)" is to find the expression of the tangent line of a function.
Newton's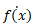
,Leibniz's
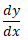,Lagrange's
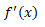,etc. Today, the Leibniz and Lagrangian styles are used.
*Important matters in business calculus
By differentiation, you can find the maximum/minimum value of profit/sales/cost/cashflow etc. The largest in the interval considered is the global maximum, maximum value, the largest in an interval is the local maximum, maximum value,the smaller is similarly the global minimum, minimum value or local minimum, minimum value. Maximums are local maxima,but local maxima are not necessarily maximums. Local maxima and minima, called extrema, are where the derivative f'(x)goes to zero. If f'(x) is+ to -, it is convex and maximum, and if it is - to +, it is concave and minimum.
For example, the graph for y=x^3-3x looks like this, but with a minimum of -2 and a maximum of +2.
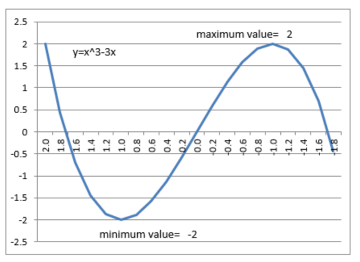
In a two-dimensional equation, the extreme value and the maximum/minimum value are the same, so if x is determined with the differentiated derivative as 0, the maximum/minimum value can be obtained.
*Important differential formula
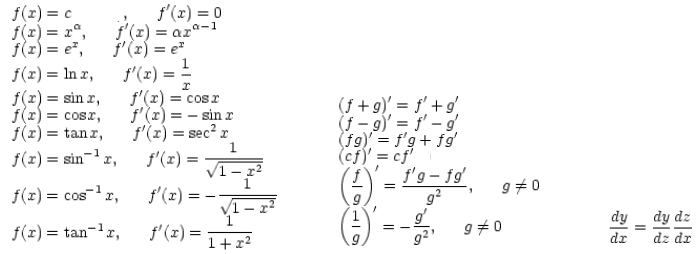c:arbitrary constant
3. Integral
Integrals can be broadly divided into two parts.
(1)Definite integral
Definite integral is a method of finding the area of a certain portion enclosed by a graph drawn by a function on a coordinate plane and coordinate axes. Any figure, no matter how complicated, can be replaced with a set of rectangular strips by slicing it into small pieces. The area of a strip is "slice width x strip height". The sum of the areas of all the strips is almost equal to the area of the figure. This is the principle of definite integral. If f(x) is the function representing the shape of the figure and dx is the width of the slice of the figure, the area of the figure can be obtained by the following formula.
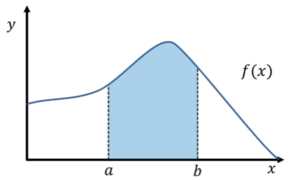
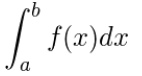
dx in the integral formula represents a very small length. Also, f(x)dx represents the product of f(x) and dx. Since f(x) is the value of f(x) at a certain point x, it can be said that it is a set of rectangles with very fine intervals between ab. If the distance between a and b is made as small as possible, the area between a and b of f(x) can be obtained. In this way, definite integral is a method of expressing the area of a certain part on a graph with a specific numerical value or variable.
(2) Indefinite integral
Another method is to find the function before differentiation by the inverse operation of differentiation. This is called finding an indefinite integral, or a primitive function.In the example below, differentiating an expression containing a constant term eliminates the constant term. From this, the constant term should appear when the integration, which is the inverse operation of differentiation, is performed.
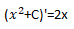differentiation
<--------> 
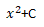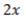
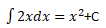integral
This constant term C is called the integration constant. This constant of integration cannot be determined by simple integration. While not determined, the constant of integration is represented by the constant symbol C.
*Important matters in business calculus
Deterministic integrals for finding areas are often used. In practice, it will be a complicated calculation, so it will not work with paper and pencil. We will use the Excel VBA-based "Definite integral by Simpson's rule"; created by our office on the Business Data page.
*Important integral formula
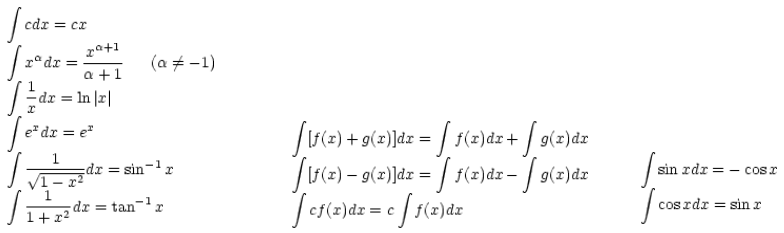
A quick note on business calculus :What was Japan like when Newton was active?
1. The history of calculus
Two important figures appear in calculus, which was established in Europe in the 17th century. Newton, the great British scientist, and Leibniz, the German philosopher and mathematician.
Newton (British:1643-1727: Died 84 years old) Leibniz(Germany: 1646-1716: Died 70 years old)
1704:Newton's"Theory of Quadrature" 1684: Leibniz's "Thesis on Calculus"
They didn't create calculus together. On the contrary, there was a fierce dispute between the academic societies in England and Germany over which of them founded calculus first. Chronologically speaking, Newton was the first to come up with the concept of calculus, but Leibniz was the first to publish it as his paper. British academics therefore accused Leibniz of plagiarizing Newton's unpublished papers. Naturally, Leibniz did not remain silent, and the exchange of violent criticism continued for many years. It is believed that he founded calculus.
Two geniuses of mathematics who lived in the 17th century, Newton died at the age of 84 and Leibniz at the age of 70. In the music world of this era, it was a little before Bach (1685-1750) of "Aria on the G string" was active. In Japan, it is the Genroku era of Tokugawa Tsunayoshi, the fifth Tokugawa shogun. That's right, calculus is "classical mathematics" that was created over 300 years ago.
2. Differentiation
Before we can understand differentiation, we need to understand limits. The limit is "to get as close to XYZ as possible". In the linear function y=x+1, if x approaches 1 as much as possible, y approaches 2 as much as possible. This is called convergence to 2, and 2 is called the limit of y=x+1.
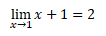
The function y=f(x) is expressed as y=f(a) when x=a. As variable x varies from a to b, y varies from f(a) to f(b).
△y＝f(a+△x)-f(a)
The average rate of change is
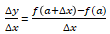.If the average rate of change converges to a constant value when △x is brought as close to 0 as possible, then this limit value is called the differential coefficient of the function y=f(x) at x=a, f' (a).f'(a)=
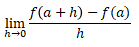
The derivative is the rate of change at point a. For y=f(x), the function f'(x) is called its derived function, and at f'(x) represent. Finding the derivative is called differentiation.
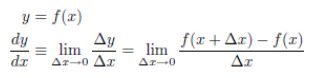
As△x approaches zero, the line approaches the tangent of f(x) at x. To "find a derivative (differentiation)" is to find the expression of the tangent line of a function.
Newton's
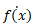,Leibniz's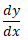,Lagrange's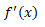,etc. Today, the Leibniz and Lagrangian styles are used.*Important matters in business calculus
By differentiation, you can find the maximum/minimum value of profit/sales/cost/cashflow etc. The largest in the interval considered is the global maximum, maximum value, the largest in an interval is the local maximum, maximum value,the smaller is similarly the global minimum, minimum value or local minimum, minimum value. Maximums are local maxima,but local maxima are not necessarily maximums. Local maxima and minima, called extrema, are where the derivative f'(x)goes to zero. If f'(x) is+ to -, it is convex and maximum, and if it is - to +, it is concave and minimum.
For example, the graph for y=x^3-3x looks like this, but with a minimum of -2 and a maximum of +2.
In a two-dimensional equation, the extreme value and the maximum/minimum value are the same, so if x is determined with the differentiated derivative as 0, the maximum/minimum value can be obtained.
*Important differential formula
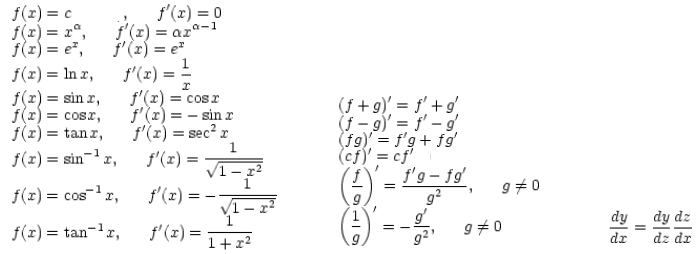c:arbitrary constant 3. Integral
Integrals can be broadly divided into two parts.
(1)Definite integral
Definite integral is a method of finding the area of a certain portion enclosed by a graph drawn by a function on a coordinate plane and coordinate axes. Any figure, no matter how complicated, can be replaced with a set of rectangular strips by slicing it into small pieces. The area of a strip is "slice width x strip height". The sum of the areas of all the strips is almost equal to the area of the figure. This is the principle of definite integral. If f(x) is the function representing the shape of the figure and dx is the width of the slice of the figure, the area of the figure can be obtained by the following formula.
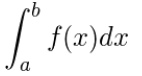
dx in the integral formula represents a very small length. Also, f(x)dx represents the product of f(x) and dx. Since f(x) is the value of f(x) at a certain point x, it can be said that it is a set of rectangles with very fine intervals between ab. If the distance between a and b is made as small as possible, the area between a and b of f(x) can be obtained. In this way, definite integral is a method of expressing the area of a certain part on a graph with a specific numerical value or variable.
(2) Indefinite integral
Another method is to find the function before differentiation by the inverse operation of differentiation. This is called finding an indefinite integral, or a primitive function.In the example below, differentiating an expression containing a constant term eliminates the constant term. From this, the constant term should appear when the integration, which is the inverse operation of differentiation, is performed.
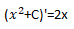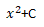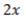
differentiation <--------> 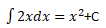integralThis constant term C is called the integration constant. This constant of integration cannot be determined by simple integration. While not determined, the constant of integration is represented by the constant symbol C.
*Important matters in business calculus
Deterministic integrals for finding areas are often used. In practice, it will be a complicated calculation, so it will not work with paper and pencil. We will use the Excel VBA-based "Definite integral by Simpson's rule"; created by our office on the Business Data page.
*Important integral formula
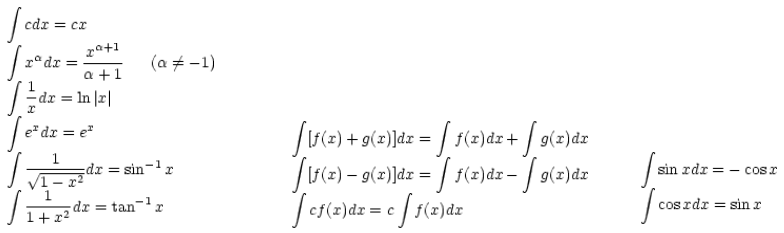
A quick note on business calculus :What was Japan like when Newton was active?