Business Calculus
Business Calculus
Business Calculus Case Study
Case example
Sales unit price of a software product series of a certain company decreases due to discount negotiations as the number of man-hours increases. Conversely, if the number of man-hours increases, the cost will rise significantly due to subcontract management costs and comprehensive debugging tests. The sales unit price and cost estimate based on the number of man-hours created in consideration of past orders received, current estimates, etc. are as follows
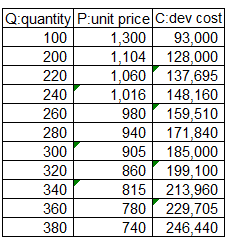

Please analyze this case by dividing it into the following steps.
STEP 1: Mathematical formula of unit price and cost due to change in man-hours
STEP 2: Trial calculation of man-hours and maximum profit by using differentiation
STEP 3: Consideration of other reference matters
***** Analysis ******
*STEP 1: Formulating the Equations for Unit Price and Cost.
We will obtain three equations using an Excel approximation curve.
・P: unit price
1)unit price line graph==> judging that linear approximation is appropriate
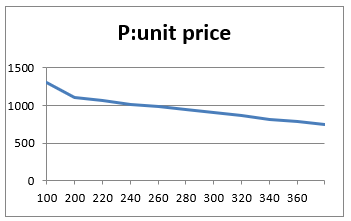
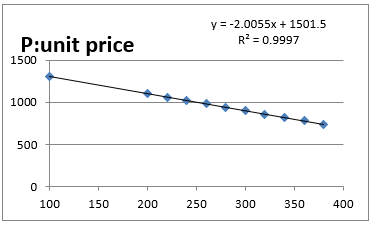
2)Selecting linear approximation from A graph
P(x)=-2.0055x+1501.5 is obtained R2=0.9997
3)effective number 2 in practice Calculated with ~3 digits∴P(x)= -2x+1500
・C: Cost
1)Cost line graph ==>Linear approximation (R2=0.9687) or polynomial approximation (R2=1.0) is a candidate, as a result of evaluation,
Determined that polynomial approximation (quadratic) is appropriate
Linear approximation Polynomial approximation
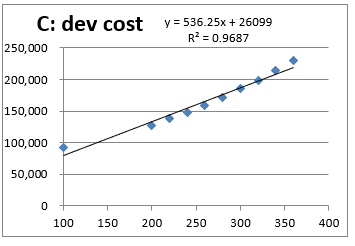
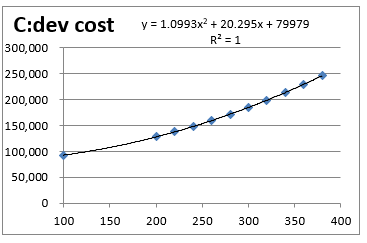
2)Select polynomial approximation (quadratic) from graph.
C(x)= 1.0993x^2+20.295x+79979 is obtained R2=1
3)In practice, calculation is performed with 2 to 3 significant digits C(x)= 1.1x^2+20x+80000
*STEP2: Calculate maximum profit using differentiation.
R: Sales R(x)= xP= x(-2x+1500)= 1500x-2x^2
C: Cost C(x)= 1.1x^2+20x+80000
P: Profit P(x)= R(x)-C(x)= 1500x-2x^2-(1.1x^2+20x+80000)
=-3.1x^2+1480x-80000
To differentiate P(x) and find the maximum value of P(x),
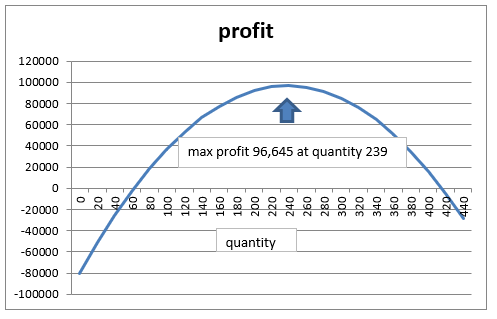
P'(x)=-6.2x+1480 x=1480/6.2=238.70≒239
P(239)=96,645 Trial calculation with maximum profit of 96,645 with 239 man- hours
*STEP3:Two break-even points.
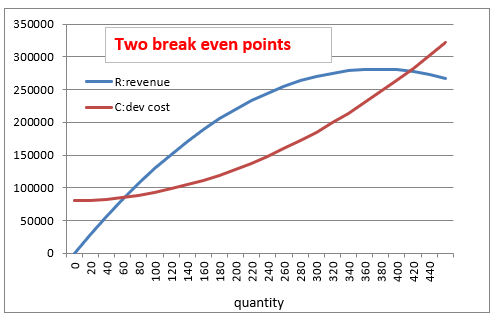
Break-even point: The point where P(x)=0 is estimated as follows.
P(x)=-3.1x^2+1480x-80000=0 The two break-even point are 62 and 415 man-hours.
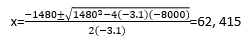
profit area for this product,
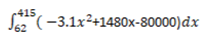
calculated by Simpson's rule
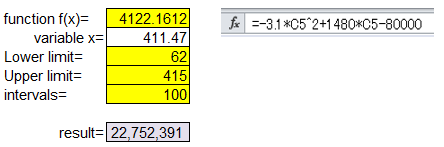
It can be said that the higher this result value is, the more profitable the product is.
In the current era of drastic changes in the business environment, it is also an effective method to compare the profit area to compare superiority with other products.
A quick note on business calculus : Maximum volume of box
Version
Case example
Sales unit price of a software product series of a certain company decreases due to discount negotiations as the number of man-hours increases. Conversely, if the number of man-hours increases, the cost will rise significantly due to subcontract management costs and comprehensive debugging tests. The sales unit price and cost estimate based on the number of man-hours created in consideration of past orders received, current estimates, etc. are as follows


Please analyze this case by dividing it into the following steps.
STEP 1: Mathematical formula of unit price and cost due to change in man-hours
STEP 2: Trial calculation of man-hours and maximum profit by using differentiation
STEP 3: Consideration of other reference matters
***** Analysis ******
*STEP 1: Formulating the Equations for Unit Price and Cost.
We will obtain three equations using an Excel approximation curve.
・P: unit price
1)unit price line graph==> judging that linear approximation is appropriate


2)Selecting linear approximation from A graph
P(x)=-2.0055x+1501.5 is obtained R2=0.9997
3)effective number 2 in practice Calculated with ~3 digits∴P(x)= -2x+1500
・C: Cost
1)Cost line graph ==>Linear approximation (R2=0.9687) or polynomial approximation (R2=1.0) is a candidate, as a result of evaluation,
Determined that polynomial approximation (quadratic) is appropriate
Linear approximation Polynomial approximation


2)Select polynomial approximation (quadratic) from graph.
C(x)= 1.0993x^2+20.295x+79979 is obtained R2=1
3)In practice, calculation is performed with 2 to 3 significant digits C(x)= 1.1x^2+20x+80000
*STEP2: Calculate maximum profit using differentiation.
R: Sales R(x)= xP= x(-2x+1500)= 1500x-2x^2
C: Cost C(x)= 1.1x^2+20x+80000
P: Profit P(x)= R(x)-C(x)= 1500x-2x^2-(1.1x^2+20x+80000)
=-3.1x^2+1480x-80000
To differentiate P(x) and find the maximum value of P(x),
P'(x)=-6.2x+1480 x=1480/6.2=238.70≒239
P(239)=96,645 Trial calculation with maximum profit of 96,645 with 239 man- hours

*STEP3:Two break-even points.

Break-even point: The point where P(x)=0 is estimated as follows.
P(x)=-3.1x^2+1480x-80000=0 The two break-even point are 62 and 415 man-hours.
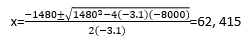
profit area for this product,
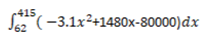
calculated by Simpson's rule

It can be said that the higher this result value is, the more profitable the product is.
In the current era of drastic changes in the business environment, it is also an effective method to compare the profit area to compare superiority with other products.
A quick note on business calculus : Maximum volume of box
Version
date |
version |
notes |
May30 2023 |
0 |
pre-released |
July1 2023 |
1 |
1st released |
Sep.30 2025 |
2 |
Updated |